Demystifying the logistic regression equation

After thinking about the whole logistic regression thing for a while, I was confused how we got to the magic e^x function considering our goal was merely to go from a crude linear approximation of a probability to a meaningful probability bounded between 0 and 1. While there are infinitely many ways to get there, here are a few arguably simpler examples I came up with to also achieve the same outcome. Notably, I was curious why we do we not use the x/abs(x) version when that gives us a much crisper binary outcome?[0]

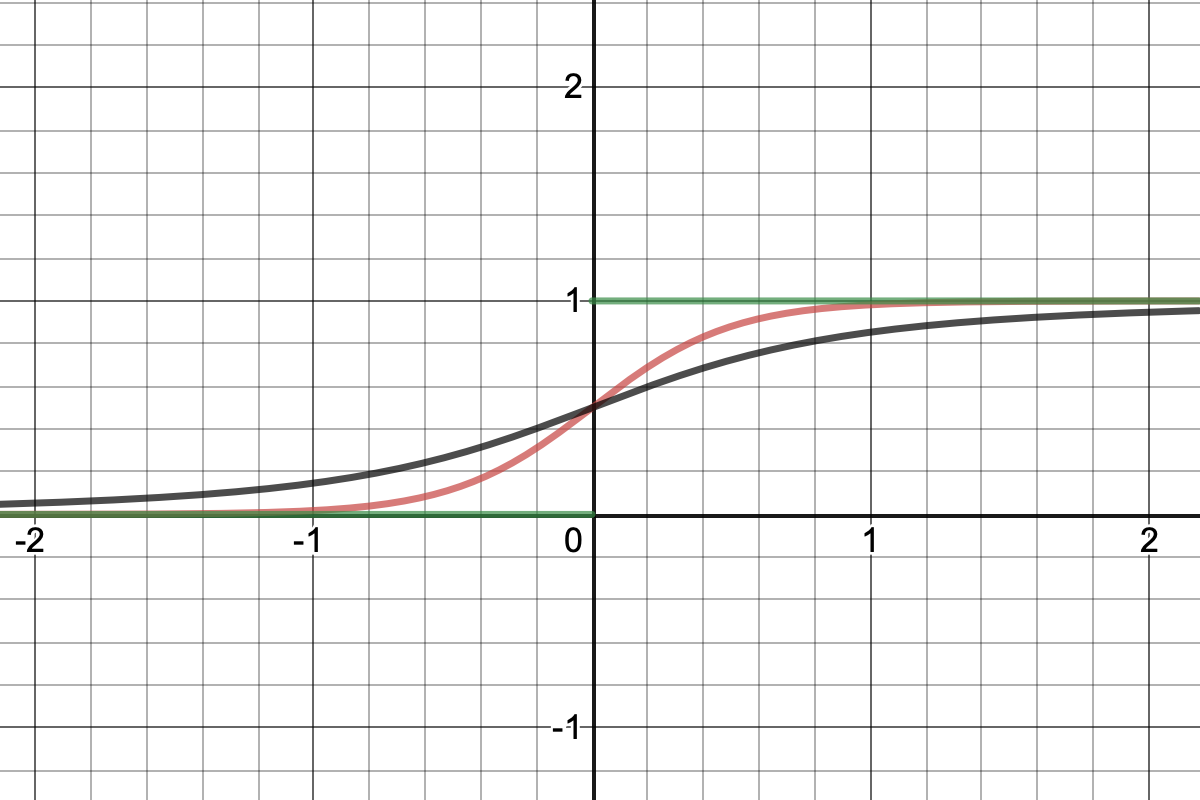
The problem breaks down into answering the following:

1. How can we make sure our output is positive?
2. And how can we make sure our output is bounded at 1?

But thinking about this, we can see that there are infinitely many ways to do this. So again, why an exponential?

I can come up with intuitions that help us understand why we use the equation we use[1]: An exponential reflects the idea that an increase in X result in an increase in p(X) and a decrease in X results in a decrease in p(X). In other words, a negative coefficient means a decrease in probability and vice versa.[2]

Exponentials? ☑ Lines? ☑ Squares? ☐ Absolute? ☐

An exponential, by definition, reflects the idea that the effect a step change in X has on p(X) depends on our current value of X.[3] In other words, if we’re considering the effect of income on probability of default, it matters whether we are going from an income of $0k–$10k vs $200k–$210k.

Exponentials? ☑ Lines? ☐ Squares? ☑ Absolute? ☐

And what about the +1 in the denominator? We could have used any number > 0. It seems 1 is just a convenient choice to help give meaning to p(X) / (1-p(X)). We could just as correctly use +2 or +3, but then we would just be carrying around a factor of 2 or 3. So we just pick +1 arbitrarily to make things simpler.

Hopefully these ramblings kind of help understand the seemingly magical appearance of e^x in this application. As with a lot of other statistical applications, the formula chosen is due to thoughtful convenience and not an absolute truth.

[0] You can just as legitimately use x/abs(x) to create your own binary classifier.

[1] These may not be the actual reasons why this equation was chosen…

[2] I guess this really just means that we want dy/dx > 0 for all x?

[3] I guess this really just means that we want d^2y/dx^2 ≠ 0?